Initialization
Our system is based on a face-centered cubic (FCC) crystal structure. This lends itself well to metallic films and substrates like Cu, Ni, Ag, Au , or Al. It can easily be extended to Si and GaAs. We begin by initializing a 2D hexagonal lattice with horizontally periodic boundary conditions. The outward facing plane is (111), and atoms are deposited on the (110) surface. A 2-dimensional system will allow us to effectively observe the strain-induced formation of dislocation and islands in a reasonable amount of time.
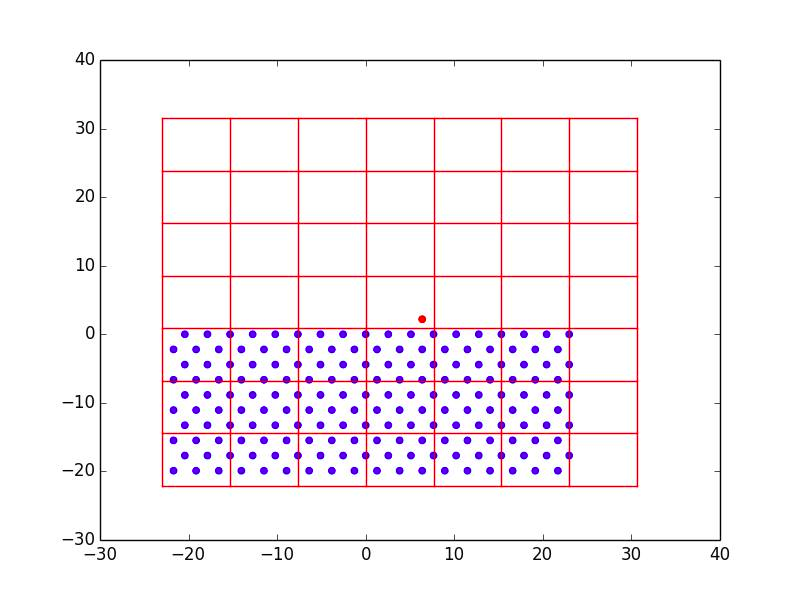
Atoms are grouped by position into boxes of size \(3r_{m}\) in order to facilitate truncation of the Lennard-Jones potential. Only atoms in the boxes neighboring the atom of interest will be included in potential energy calculations. For \(r_{ij}>3r_{m},\, U_{ij}\) is within \(0.003 \, \varepsilon_{ij}\) of zero, so this saves a significant amount of computation time with very minimal sacrifice of accuracy. Figure 1 shows the (111) plane of the binned substrate with the first deposited atom on top. In order to avoid additional interfacial diffusion effects, we only allow the top layer of substrate atoms to move. Since there are no surface atoms in the very beginning, it is assumed that the deposition probability is 1. The first atom is just deposited randomly and relaxed into position without any additional rate calculations.
Algorithm:
The growth algorithm can be summarized in the following block diagram:
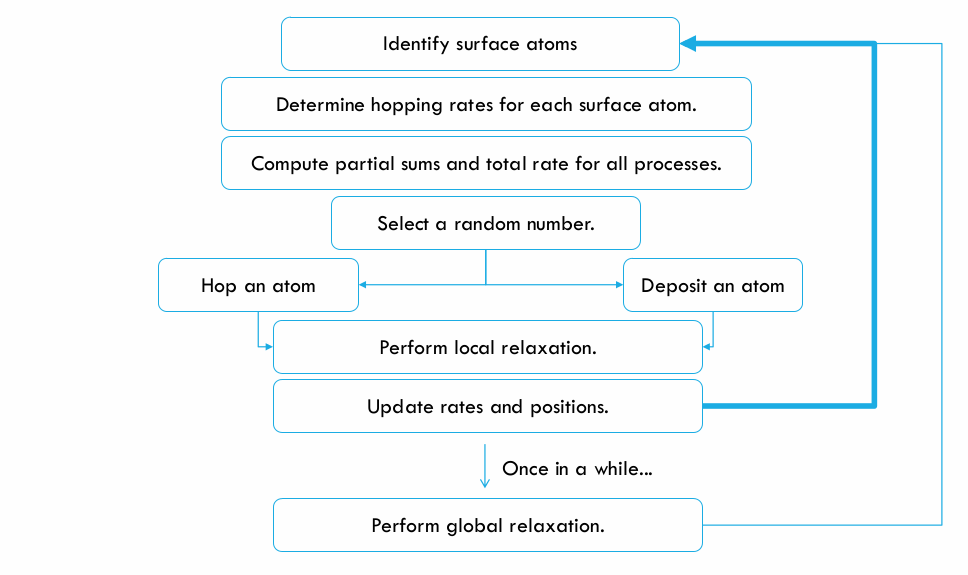
Identification of Surface Atoms
Surface atoms are defined as any adatom that is coordinated by less than five nearest neighbors. As afore stated, substrate atoms are excluded from this list. Surface atoms are indicated by red dots in our figures. Fully coordinated atoms have six nearest neighbors, and are indicated by green dots.
Determining Hopping Rates
For each identified surface atom, the hopping rate is calculated as in Equation [eq:3]. We set the attempt frequency, \(\omega,\) equal to the rate of unhindered diffusion for a surface atom on a lattice: approximately \(10^{12}s^{-1}.\) \(k_{B}=8.617\times10^{-5}eV/K\). Temperature may be varied.
It was mentioned that \(\Delta U\) would be approximated by a pseudo-bond-counting method:
\[\Delta U=\Delta U_{approx}-(\Delta U_{loc}-\Delta U_{loc}^{ideal})\]
where$\Delta U_{approx}$ is the energy needed to completely remove an atom from its current configuration. This is calculated by summing the Lennard Jones potential over all the atoms in adjacent bins. \(\Delta U_{loc}^{ideal}\) would be equivalent to the sum of the ideal energies in each of the local (nearest neighbor) bonds. For a surface atom coordinated by \(N_{s}\) nearest substrate neighbors and \(N_{a}\) nearest adatom neighbors,
\[\Delta U_{loc}^{ideal}=-(\varepsilon_{a-s}N_{s}+\varepsilon_{a}N_{a})\]
On the other hand, \(\Delta U_{loc}\) is the actual energy stored in the local bonds. It is calculated by summing the Lennard Jones potential over nearest neighbor atoms only. Therefore, the quantity \((\Delta U_{loc}-\Delta U_{loc}^{ideal})\) accounts for lattice strain energy. For a relaxed homoepitaxial system, \(\Delta U\approxeq\Delta U_{approx}\).
Total Rate and Choosing an Event
Once the hopping rates are computed for all N surface atoms, the partial sums
\[p_{j}=\sum_{i=1}^{j}r_{i}\]
should be computed and stored. This yields a continuum of N hopping probabilities like the ones labeled in Figure 1 for N=3. The total rate is given as in ([eq:2]).
To choose an event, a random number \(u\in(0,R_{total})\) is selected from a uniform distribution. If
\[\begin{cases}u < p_{j}, & \mathrm{Hop \, atom \, j}\\ u > p_{N}, & \mathrm{Deposit \, an \, atom}\end{cases}\]
Hopping
If an atom is chosen to hop, one surface atom is chosen at random from the adjacent bins. The potential, U(x), is then calculated at each of the 6 positions coordinating the chosen atom. The hopping atom moves to the position with the lowest energy. Finally, a local relaxation is performed around the destination using the nonlinear conjugate gradient method.
Deposition
If deposition is chosen, a random position is chosen within the bounds of the maximum film height and width. This position could end up being 10 layers above the surface, which would take a long time to relax. To accomodate this possibility, the adatom is moved down by \(r_{a}\) every time it finds itself more than \(2r_{a}\) away from any other atoms. When it is finally within range, a local relaxation is performed using the nonlinear conjugate gradient method.
Local vs Global Relaxations
Relaxations using the nonlinear conjugate gradient method are performed to find the minimum energy positions of particles after hopping or deposition events. A local relaxation of just the atoms within \(3 \, r_m\) of where the event occurred should be sufficient to find a new local minimum energy configuration within the threshold force value discussed previously. If the local relaxation causes atoms to move outside of this radius or causes atoms outside of the relaxation scope to experience forces greater than the threshold, then a global relaxation of all atoms is performed. Additionally, if the change in force from step to step is too small the the relaxation has lost conjugacy. In this case, the step size of the line search is halved and the relaxation step is performed again from the beginning. Our implementation of the local relaxation process was unstable, so only global relaxations were performed. Although this dramatically increased the computation time required for each step, it helped prevent forces from becoming too large.