Currently, we are able to work with just about 30 atoms before issues with the nonlinear conjugate gradient algorithm implementation prevent our atoms from settling into a local minimum energy configuration. Due to this bug, we sometimes allowed the first layer of substrate to diffuse so we had more atoms to observe.
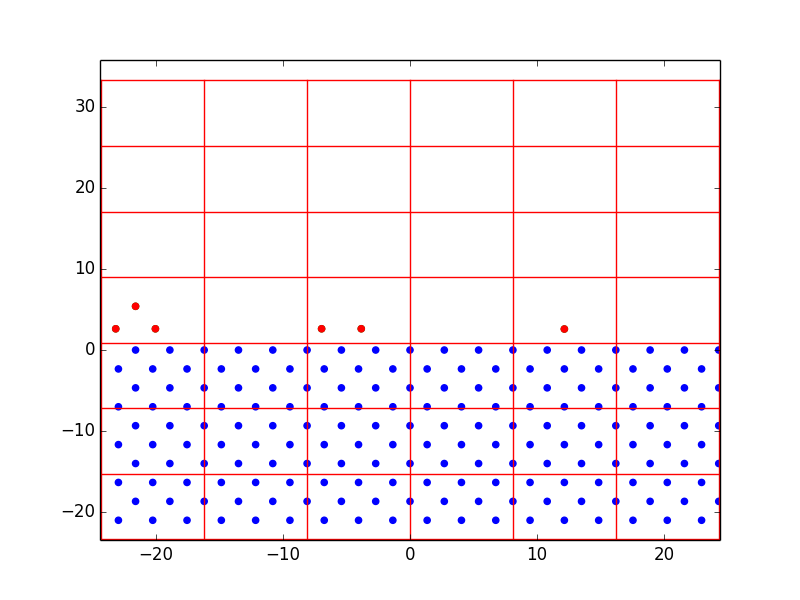
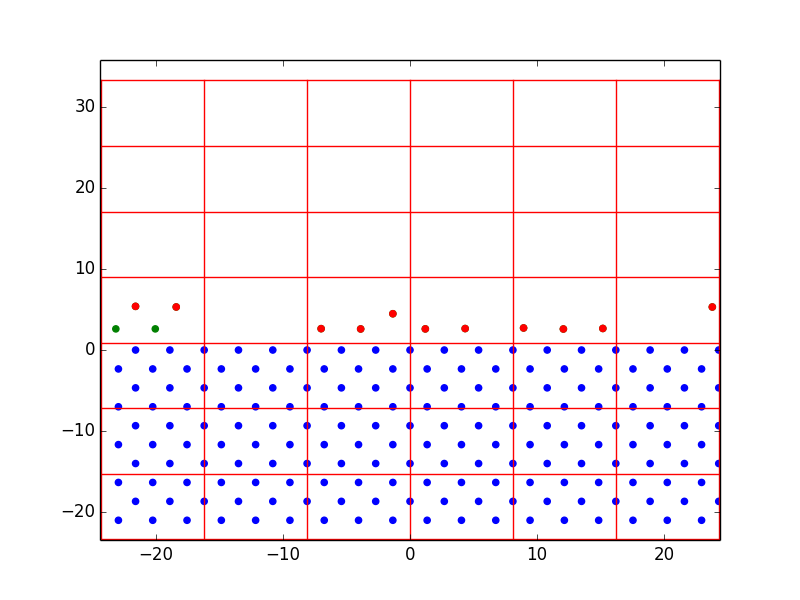
Nevertheless, we were able to learn a lot from just a few rough layers. Figure 1 shows the progression of homoepitaxial film growth over 14 steps, beginning with 18 diffusion-enabled substrate atoms. We first set the lattice parameters and bond energies equal to prove the concept of off-lattice KMC. It was observed that atoms were preferentially deposited over the first five steps, and hopping was finally chosen at step 6. After that, hopping began to dominate over deposition. This demonstrates the desired effect of the rate-equation KMC model; surface diffusion occurs on the order of \(10^{12} s^{-1}\) while deposition in a region as small as this might only occur at \(10 s^{-1}\). A surface atom in a monolayer has four nearest neighbor bonds, therefore there is a large activation energy barrier to move to a site with only one or two bonds. By equation [eq:1], the calculated hopping rate would be very small, and therefore the n-fold method is very likely to choose deposition. But once there are more surface atoms hanging around – some with few bonds and very low activation energies – the hopping probability increases significantly. The more surface atoms, the more hopping dominates until they all form bonds with each other and deposition is favored once again.
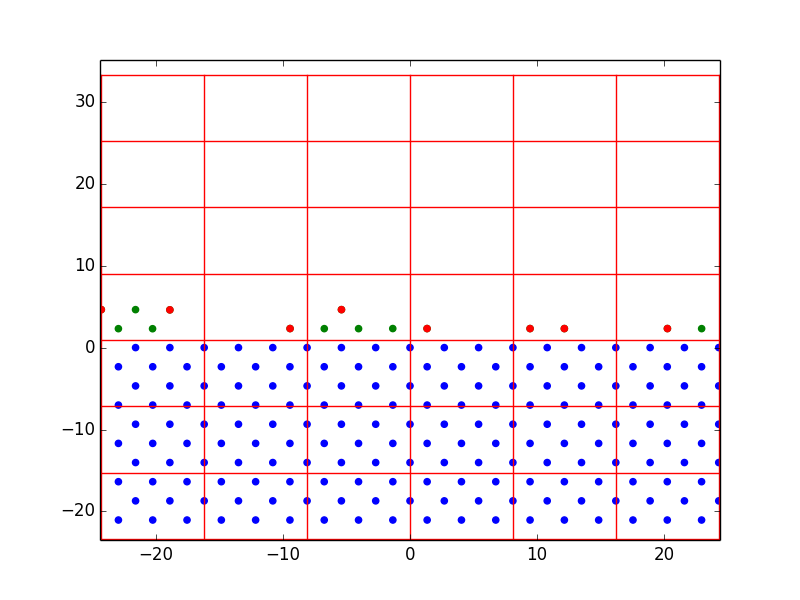
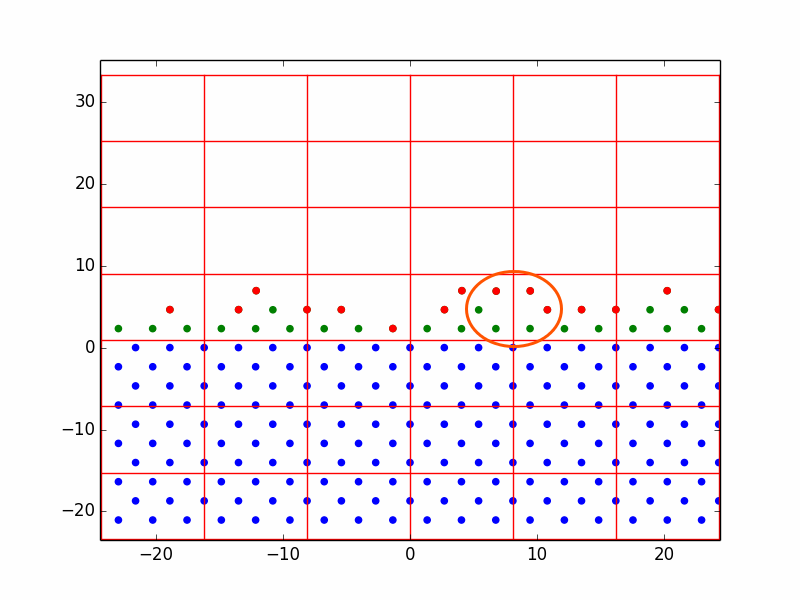
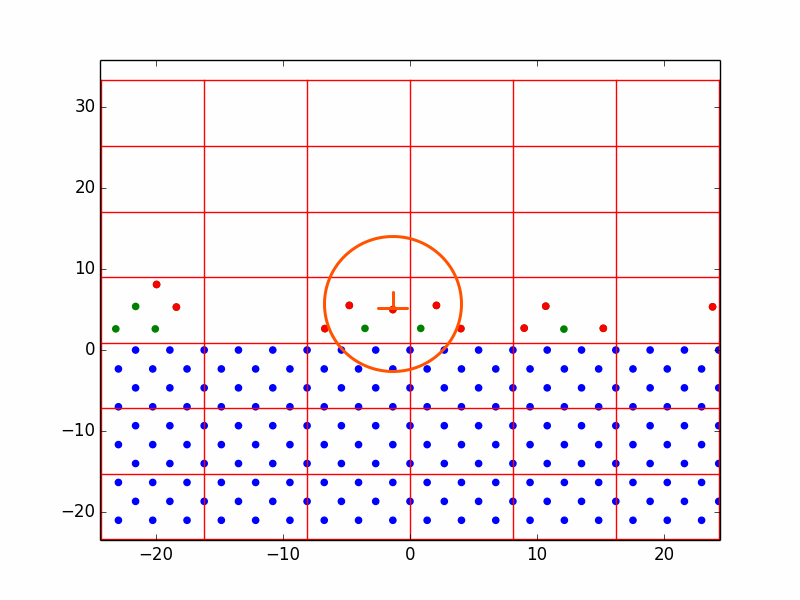
In one run with the homoepitaxial parameters, we observed the process of vacancy formation. The vacancy in Figure 2 is circled in orange. This was the result of random deposition events. Because of the process described in 4.2.5, atoms are rarely deposited directly onto the surface. Instead, they are gradually shifted down from above until they are close enough to be acted upon by the nonlinear conjugate gradient. They settle in the first configuration that is energetically favorable, which is not necessarily the close-packed configuration. It is probable that this vacancy would diffuse and/or disappear over time.
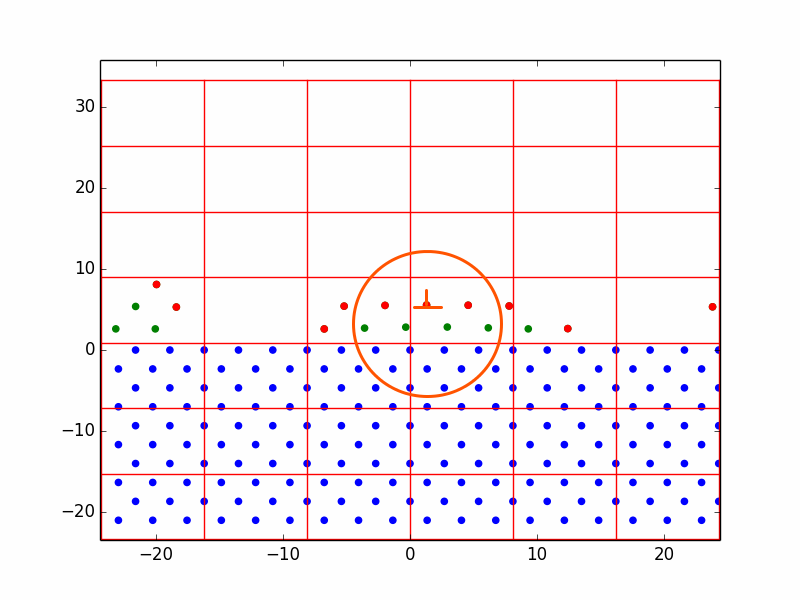
When attempting to simulate heteroepitaxy, we were obliged to induce very large lattice misfit. Otherwise, due to bugs, we would not create enough layers to observe dislocation formation. The silver-on-copper system has an 18.5% misfit, which was theorized to form dislocations at the very first layer (the VM growth mode). Results are shown in Figure 3. In this case, we did not allow the substrate atoms to diffuse. It was observed that adatoms deposited far from other adatoms were nicely centered between the substrate atoms below, but the introduction of a nearby adatom forced both of them off-center of the lattice site. In Figure 3, an attempt to deposit an adatom between two existing adatoms resulted in the beginnings of a dislocation. It found a lower energy position just above the first layer plane. As more adatoms were deposited nearby, the dislocation became incorporated into the lattice.
As mentioned, future work is required to simulate more than about 30 atoms. Our current implementation often fails to find a local minimum energy configuration if the number of mobile atoms is too high. The forces on each atom are above the threshold value of \(10^{-2}\) eV / \(\buildrel _\circ \over {\mathrm{A}}\) and fails to converge. The calculations themselves are clearly working, as small numbers of atoms easily find the minimum energy configuration. Perhaps another formalism for the conjugate step size would be more appropriate for this problem.
Images of other results can be found on GitHub.